Opis

Pan B. wyjeżdża dzisiaj z żoną na wakacje (nad morze, do ciepłych krajów). Niestety szef kazał mu załatwić parę spraw na mieście przed wyjściem z pracy. Musi wykonać polecenie szefa, albo będzie to jego ostatni dzień w pracy. Z drugiej strony, bilet na samolot już został wykupiony, więc Pan B. musi załatwić te sprawy jak najszybciej. Zaznaczył więc sobie na mapie punkty, w których ma coś do załatwienia oraz sprawnie oszacował czas przejazdu między każdą parą z nich. Dodatkowym utrudnieniem jest fakt, że pewne sprawy musi załatwić przed innymi. Na przykład, żeby dostarczyć ubrania szefa do pralni musi najpierw podjechać do jego domu. Wcześniej musi jednak odebrać żonę szefa od fryzjera. Żeby to zrobić musi najpierw pobrać w banku pieniądze z firmowego konta, by mieć czym zapłacić fryzjerowi. Do tego jednak potrzebuje firmową kartę kredytową, którą szef zostawił w domu swojej ko…leżanki.

Pan B. ma jednak łeb na karku (za to mu płacą) i szybko uwinął się z zadaniem. Zaraz potem przyjechał zziajany do domu i co się okazało? Okazało się, że żona jeszcze ich nie spakowała, bo nie wie które sukienki ze sobą zabrać. Tak to już niestety w życiu bywa, że walizki mają ograniczoną pojemność i nie wszystko można zabrać ze sobą. Państwo B. ustalili więc wartość użytkową, tj. przydatność, przedmiotów kandydujących do spakowania (przykładowo perfumy i kosmetyki są bardziej przydatne niż płyn na komary, a sukienki niż stroje kąpielowe). Teraz Pan B. musi zapakować te przedmioty, których sumaryczna wartość użytkowa jest maksymalna.

I z tym problem Pan B. szybko sobie poradził. Pobiegli więc z żoną do taksówki. Taksówkarz jednak był początkujący i nie znał dobrej trasy na lotnisko, a czasu już wiele nie zostało. Trzeba więc było mu wskazać najszybszą trasę przy uwzględnieniu korków, robót na drodze, sygnalizacji świetlnych i pozycji patroli policyjnych.

Do odlotu już coraz mniej czasu, ale Państwo B. szczęśliwie dojechali na miejsce. Trzeba jeszcze zapłacić za taksówkę. Pan B. miał przy sobie tylko bardzo grube banknoty, dał więc jeden kierowcy. No i powstaje pytanie czy taksówkarz będzie w stanie wydać mu resztę, co do grosza, z posiadanych przez siebie monet i banknotów (Pan B., jako rodowity Poznaniak, nawet nie rozważał możliwości dania napiwku). Co więcej, jeśli resztę się dało wydać, to trzeba było zrobić to jak najmniejszą liczbą monet/banknotów, żeby zminimalizować czas potrzebny na przekazywanie pieniędzy i obliczanie sumy.

Uporawszy się z płatnościami za taksówkę Państwo B. wbiegli na lotnisko. Teraz stanęli przed problemem wyboru kolejki do odprawy. Nie zawsze wybór najkrótszej kolejki jest optymalny, bo w niektórych stoją większe grupki (rodziny, wycieczki, itp.), które sumarycznie obsługiwane są szybciej. Wybrali więc jakąś kolejkę i jak się okazało najszybciej dotarli do stanowiska obsługi. A jak już dotarli to się okazało, że Pan B. zapomniał wziąć z domu bilety.

Ciężkie jest życie Pana B. — nie spodziewał się, że będzie to najbardziej szalony dzień jego życia. Ale to zadanie jest zupełnie nie o tym. Otóż Pani C., która nigdy nie miała takich problemów, ani nawet nigdy nie miała okazji spotkać się z Panem B., postanowiła rozwiązać totalnie nieżyciowy problem, który wymyśliła z nudów siedząc w pracy i grając w pasjansa. Mianowicie, mając ciąg liczb A1, A2, …, AN oraz serię par (p,h), chciałaby dla wszystkich tych par sprawnie obliczyć poniższą sumę.

Zadanie

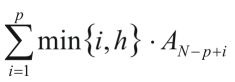
Dany jest ciąg oraz pary liczb całkowitych. Dla każdej pary wylicz odpowiednią sumę, wyznaczoną przez tę parę, w ciągu.

Specyfikacja wejścia

Pierwsza linia wejścia zawiera liczbę całkowitą D (1 ≤ D ≤ 50), oznaczającą liczbę zestawów danych. Pierwsza linia każdego zestawu danych zawiera liczbę całkowitą N (1 ≤ N ≤ 100000), będącą długością ciągu. Druga linia zawiera liczbę całkowitą K (1 ≤ K ≤ 50000), oznaczającą liczbę par. W trzeciej linii zestawu znajduje się N liczb całkowitych: A1, A2, …, AN (–100000000 ≤ Ai ≤ 100000000 dla i = 1…N). Kolejne K linii zawiera pary liczb całkowitych p i h (1 ≤ p, h ≤ N).

Specyfikacja wyjścia

Dla każdego zestawu należy wypisać jedną linię zawierającą K liczb całkowitych, oddzielonych spacjami, będących wynikami odpowiednich sum, dla każdej z par (p,h) podanej na wejściu. [ Uwaga! Liczby te mogą nie mieścić się w 32-bitowym typie całkowitym. Zalecamy użycie typu long long w C/C++ oraz int64 w Pascalu — są to typy 64-bitowe. ]

Przykład

Wejście

Wyjście

3 10 3
13 21 34 55